论文信息

标 题：Thermodynamic-based constitutive model of hot dry rock after cooling

期刊：International Journal of Mechanical Sciences

第一作者：Zhen Wang (汕头大学 土木与智慧建设工程系)

通讯作者：Ming Wu 吴鸣 教授 (汕头大学 土木与智慧建设工程系)

其他主要作者：Shu Zhu 朱姝 副研究员 (河海大学 岩土力学与堤坝工程教育部重点实验室; 江苏省岩土工程技术工程研究中心); Zhen-de Zhu 朱珍德 教授 (河海大学 岩土力学与堤坝工程教育部重点实验室; 江苏省岩土工程技术工程研究中心)

DOI: https://doi.org/10.1016/j.ijmecsci.2025.110461

Online日期：2025.06.12

摘要

干热岩经历冷却热冲击（TSC）后的残余强度对地热开采过程中井筒完整性的维持具有重要意义。值得注意的是，大多数干热岩的残余强度在初始温度升高时表现出非单调变化规律。传统损伤力学虽能模拟强度的单调退化，但难以准确刻画这种非单调行为。

为解决该问题，本文提出了一种基于热力学的本构模型，通过引入热-应力场之间的相互影响机制，成功模拟了残余强度的非单调变化过程。该模型采用昂萨格倒易关系（Onsager reciprocal relations）建立热力学耗散约束矩阵，为构建考虑物理场相互作用的热力学本构关系提供了理论基础。

该模型既可模拟残余强度的非单调变化，也适用于单调退化情形。通过调节物理场间的相互作用系数，模型能够实现从单调到非单调的行为转变。与传统损伤模型中人为设定“正/负损伤”共存的假设不同，本方法提供了更具物理基础的途径，用于处理实际工程中单调与非单调损伤并存的复杂工况。该模型可作为地热开采中井筒稳定性分析的数值计算工具，并为多物理场耦合下岩石行为的研究提供新的思路。

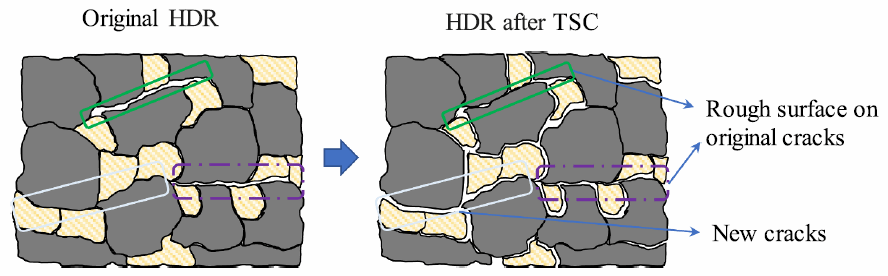
Fig. 2. Rocks are composed of two mineral components, represented by yellow (with diagonal shading) and gray, respectively. When subjected to thermal shock, the thermal expansion coefficients of the two minerals are different. Cracks will occur at the boundaries of different minerals. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

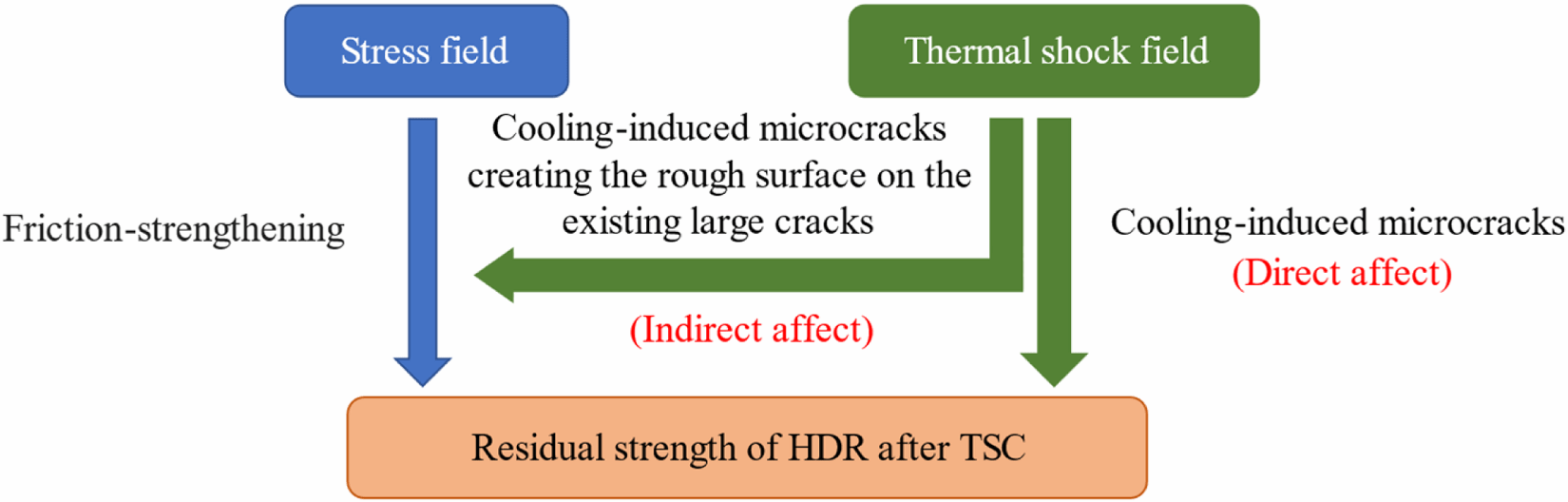
Fig. 3. The direct and indirect influences of the thermal shock field. the influence of the thermal shock field on HDR’s residual strength comprises two components: (1) Cooling-induced microcracks form at the boundaries between minerals which degrade the structural integrity of HDR, thereby directly affecting its residual strength; (2) Cooling-induced microcracks creating the rough surface on the existing large cracks which enhance friction of cracks and affect the stress field, thereby indirectly affecting HDR residual strength through the stress field.

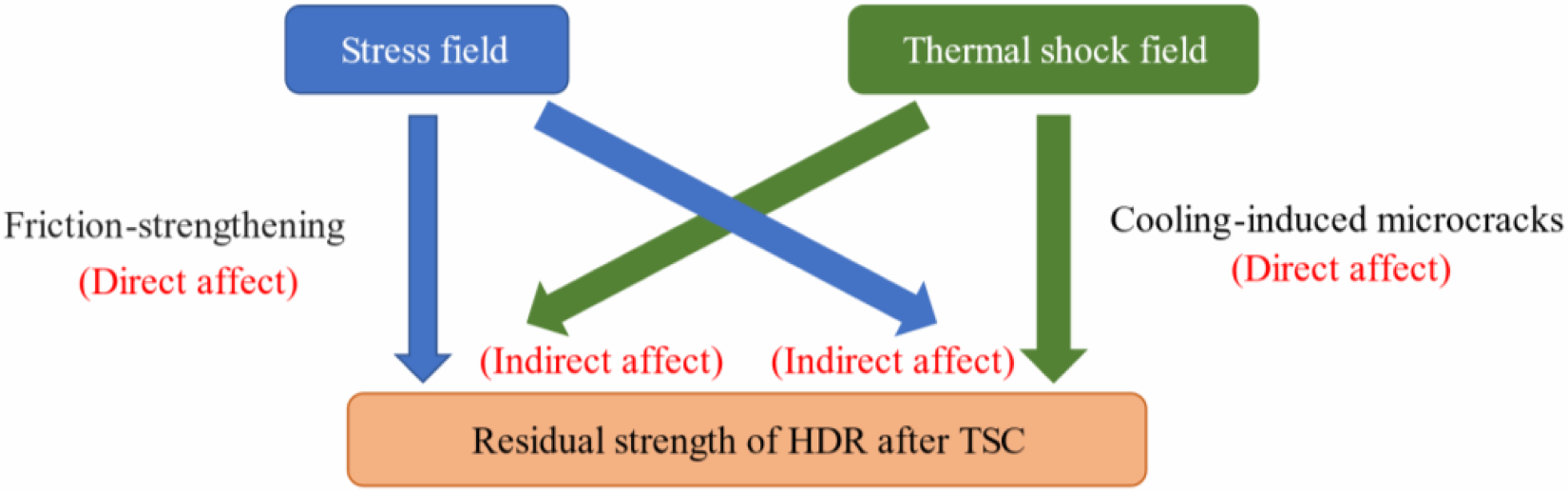
Fig. 4. The coupling effect between the stress field and the thermal shock field. According to the Onsager reciprocal relations, the coupling effect between the thermal shock field and the stress field must account for both the indirect influence of the thermal shock on the stress and the indirect influence of the stress on the thermal shock.

Fig. 5. The processes of establishing thermodynamic constitutive model of HDR after TSC. The derivation consists of five steps: intrinsic variable, thermodynamic force, thermodynamic state potential, thermodynamic dissection potential, and thermodynamic-based constitutional model.

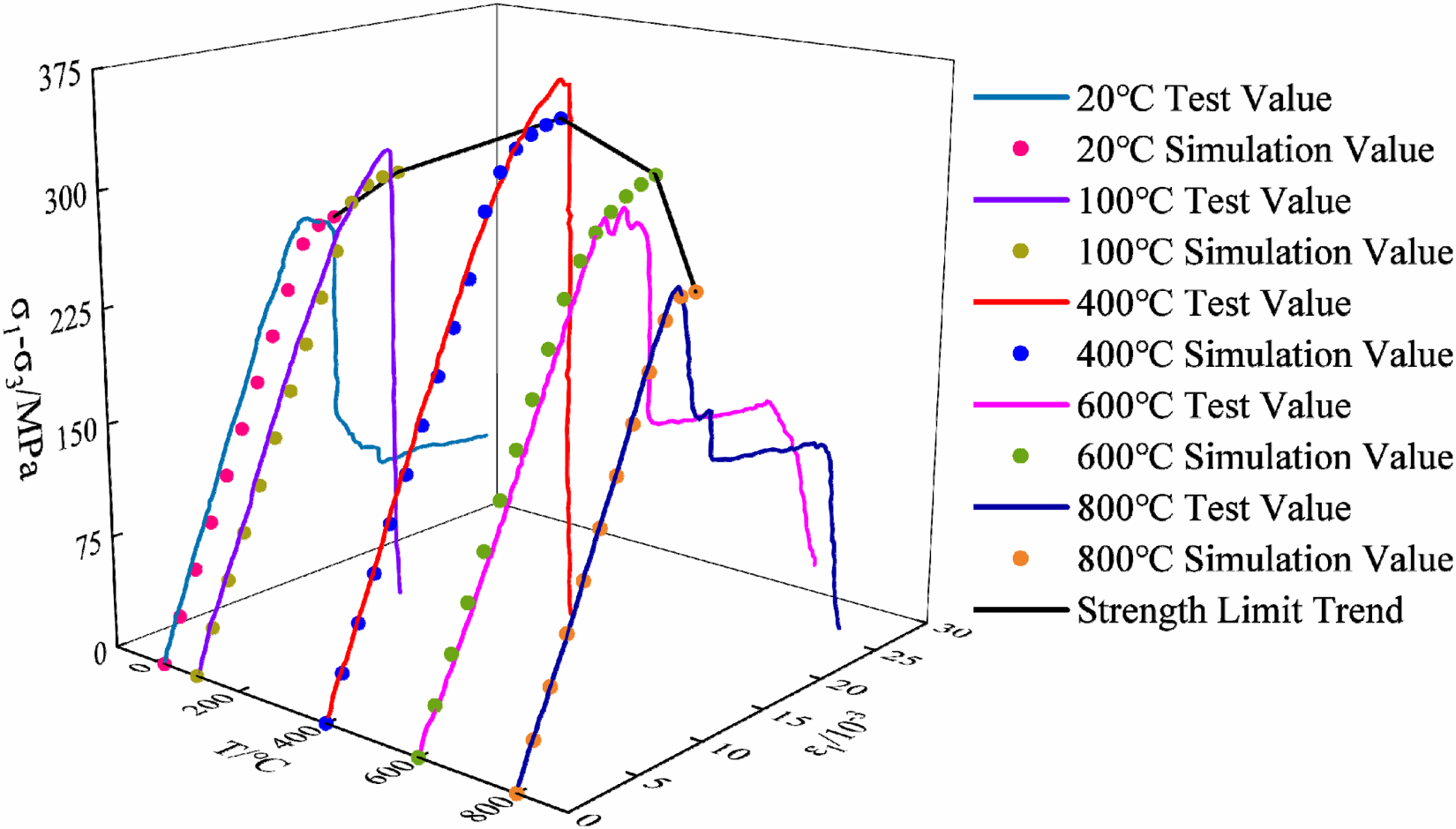
Fig. 6. Comparison between simulation and test results at different original temperatures (20◦◦C, 100◦◦C, 400◦◦C, 600◦◦C, 800◦◦C). Experimental data (solid line) adapted from Author Li et al. [31]. The solid lines representing temperatures of 20◦◦C, 100◦◦C, and 400◦◦C show that the residual strength gradually increases as the original temperature rises. The solid lines representing temperatures of 600◦◦C and 800◦◦C demonstrate that residual strength decreases as the original temperature increases. The simulation results are represented by scatter points. The simulation results reproduced the above experimental characteristics very well.

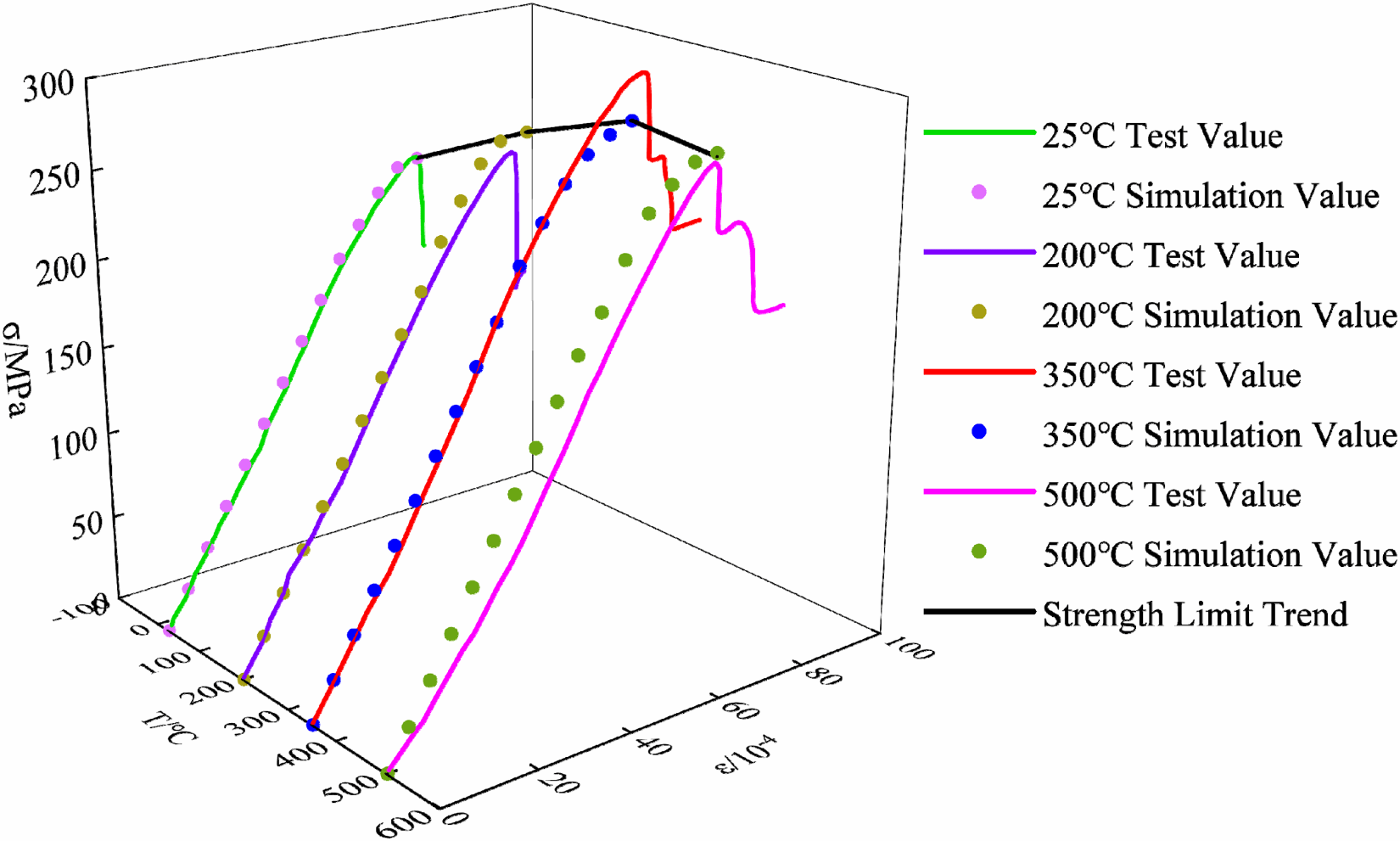
Fig. 7. Comparison between simulation and test results of sandstone at different original temperatures (25◦◦C, 200◦◦C, 350◦◦C, 500◦◦C). Experimental data (solid line) adapted from Author Li et al. [38]. Experimental results for sandstone are depicted using solid lines, with peak residual strength observed at 400◦◦C. Scatter points denote simulation outcomes. The computational model accurately replicates the experimental phenomenon where maximum residual strength occurs at this critical temperature threshold.

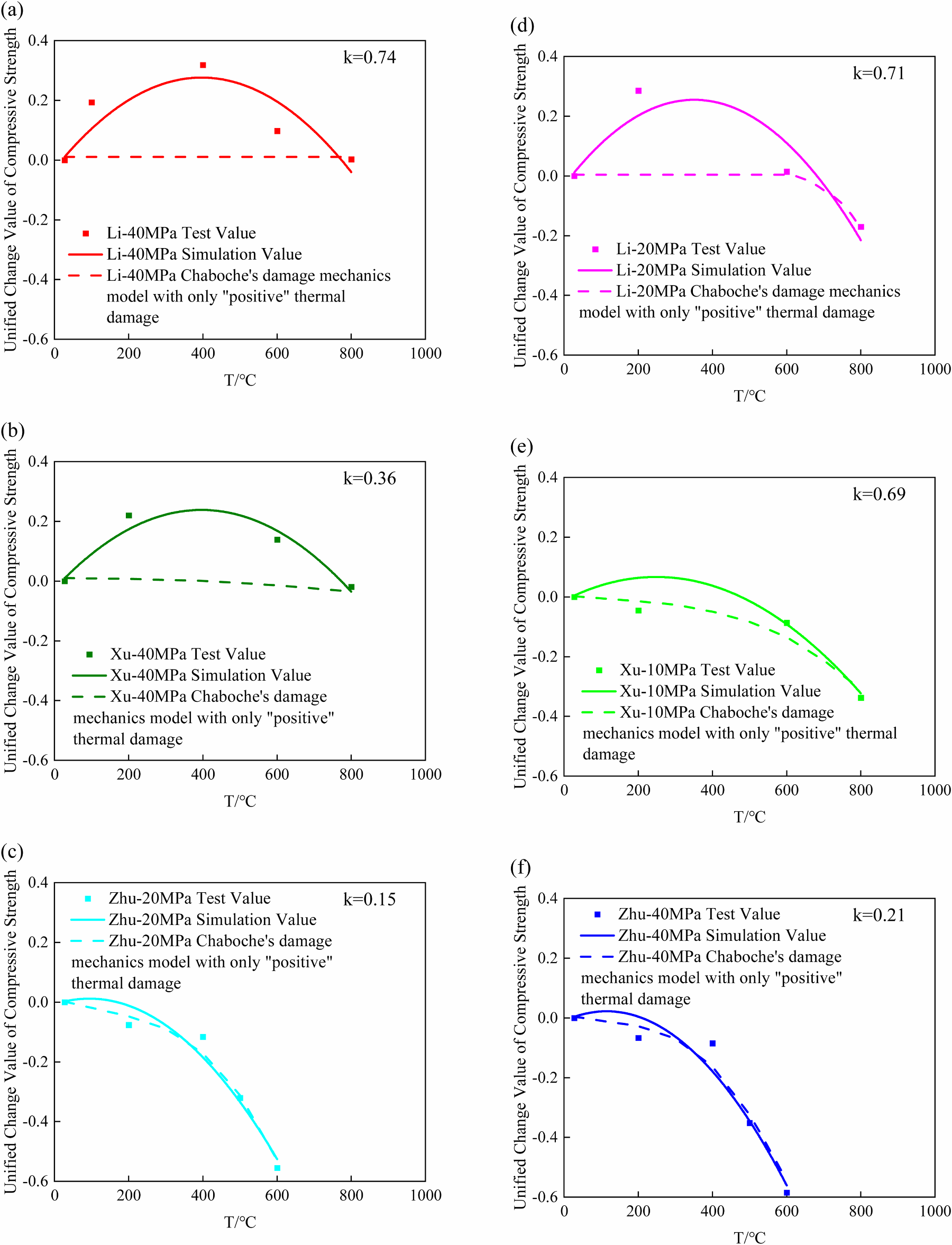
Fig. 8. Simulated comparison of unified change value of compressive strength and multiple physical fields mutual influence coefficien k(Fig. a, d cited from Li et al. [31], Fig. b, e cited from Xu et al. [64], Fig. c, f cited from Zhu et al. [32]). In Fig. 8 (a) and (d), residual strength exhibits a non-monotonic variation of first increasing and then decreasing as original temperature increases. In this paper, the non-monotonic of residual strength is caused by the mutual influence between thermal shock field and the stress field. Therefore, the mutual influence coefficient ̃k, which reflects mutual influence between the thermal shock field and the stress field, should theoretically be different. Indeed, the coefficient ̃k obtained from the 6 sets of test are indeed different. A greater mutual influence corresponds to a larger value of ̃k. The Chaboche damage model accurately captures the monotonic reduction of residual strength with thermal shock temperature observed in Zhu’s experiments. However, it exhibits marked discrepancies when addressing the non-monotonic residual strength evolution patterns observed in Li’s and Xu’s experiments.

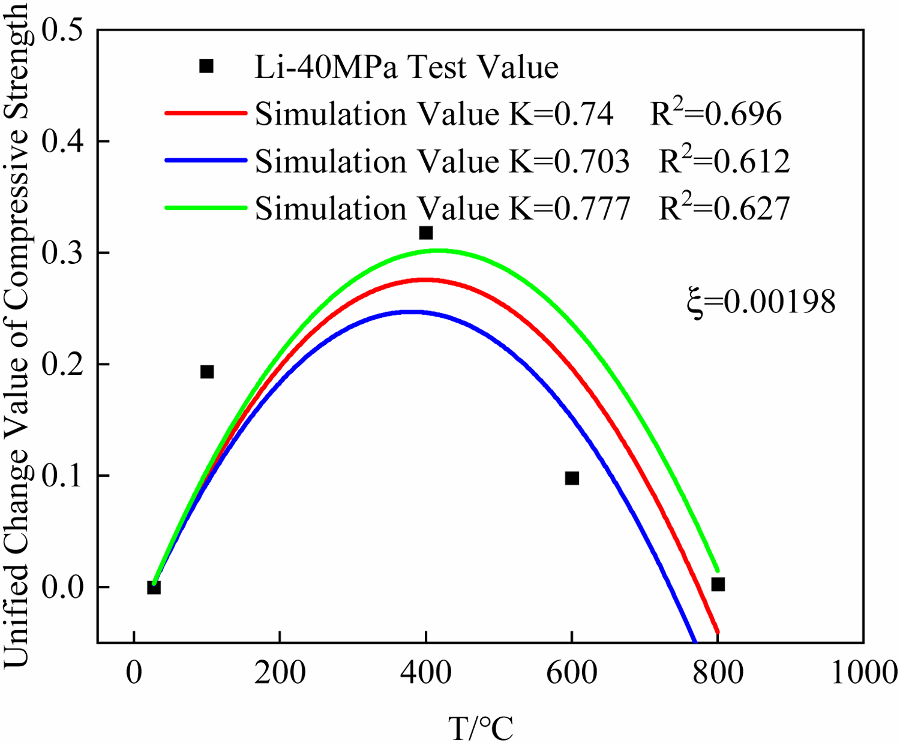
Fig 9. The residual strength simulation under ±5 % parameter ̃k deviation from its optimal value. The red curve corresponds to the baseline scenario with optimal parameter settings (k=0.74). The green curve demonstrates residual strength simulation under a 5 % parameter increase (k=0.777), while the blue curve characterizes the behavior with a 5 % parameter reduction (k=0.703). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

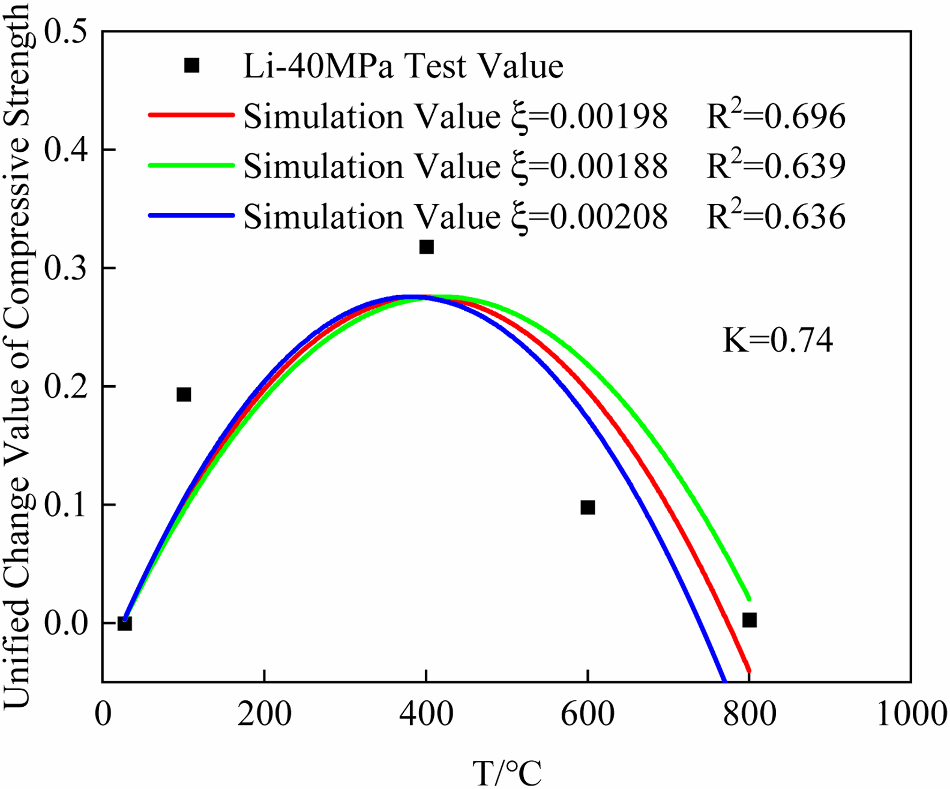
Fig 10. The residual strength simulation under ±5 % parameter ξ deviation from its optimal value. The red curve corresponds to the baseline scenario with optimal parameter settings (ξ=0.00198). The green curve demonstrates residual strength simulation under a 5 % parameter reduction (ξ=0.00188), while the blue curve characterizes the behavior with a 5 % parameter increase (ξ=0.00208). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

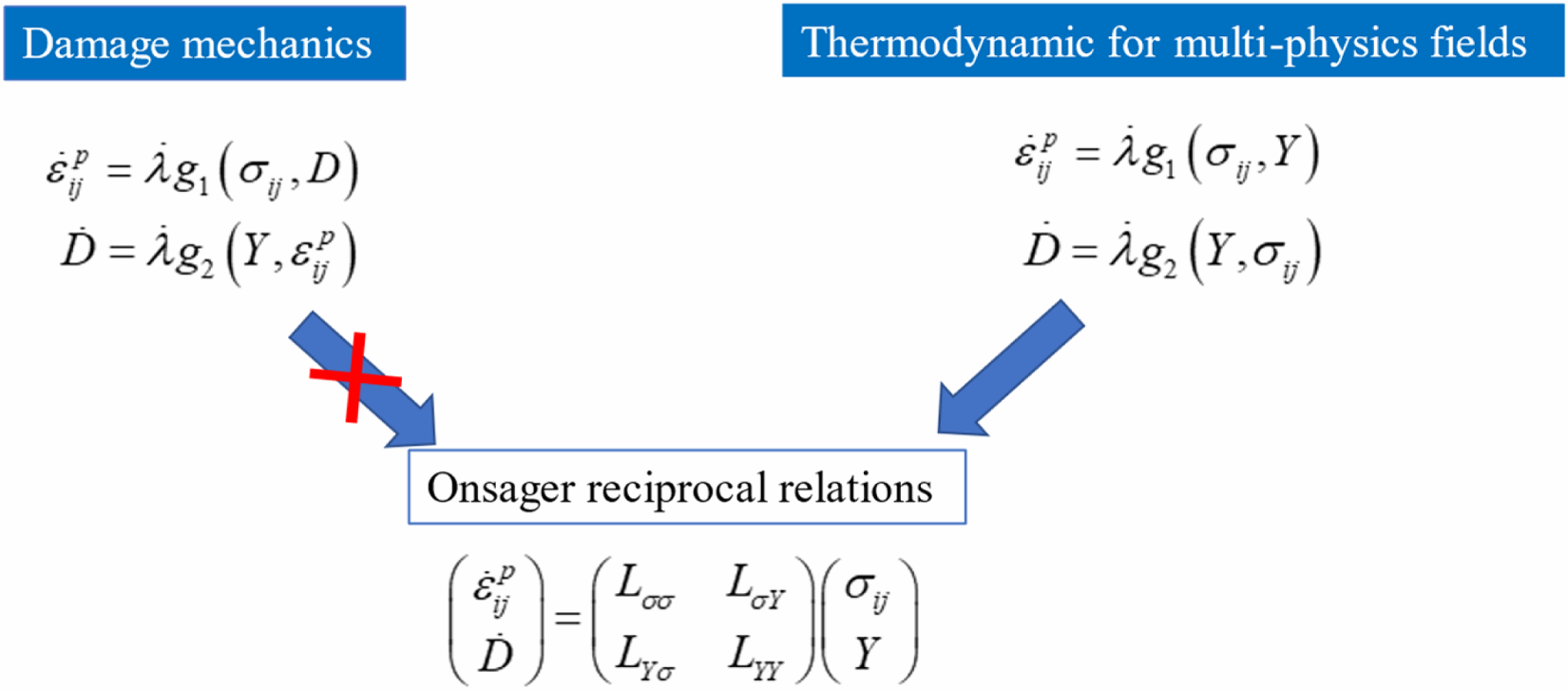
Fig. 11. The difference with damage mechanics. When traditional damage mechanics is employed to establish coupled-field evolution equations for thermodynamic flows, the thermodynamic flows are governed by both thermodynamic forces and state variables. However, under rigorous thermodynamic frameworks, such evolution equations where flows are co-determined by forces and state variables fail to satisfy the Onsager reciprocal relations. This arises because the Onsager formalism strictly requires thermodynamic flows to be exclusively controlled by thermodynamic forces. In the proposed multi-physics thermodynamic framework, thermodynamic flows are solely governed by thermodynamic forces, thereby rigorously satisfying the Onsager reciprocal relations.

结论

HDR经历热冲击冷却（TSC）后的残余强度演化过程复杂，表现为单调与非单调行为交织的特征。传统损伤力学虽可有效描述强度的单调衰减，但难以应对非单调演化的情况。本文通过三个层级的理论进展，建立了一个新的分析框架，克服了该领域的关键建模难题。

首先在机理层面，本文指出：将非单调行为简单归因于热冲击引起的“强化阶段”的传统解释无法准确反映热-力耦合过程中的场间相互作用。为此，本文提出了物理场间双向耦合机制，明确区分了直接的热冲击效应与其对应力场的间接影响，构建了全新的解释框架，从根本上重新诠释了HDR残余强度的非单调演化规律。

在此理论基础上，本文进一步建立了一个创新的热力学本构模型，系统纳入了多物理场间的交互耦合效应。模型的核心在于基于昂萨格倒易关系构建的耗散约束矩阵，该矩阵以能量耗散为约束替代了传统模型中经验性的“恢复性损伤”假设，保证了热力学一致性与物理合理性。通过调节“物理场互作系数”，该模型可灵活模拟残余强度的单调退化与非单调回弹过程，突破了传统“正/负损伤共存”模型的理论瓶颈。

在实验验证方面，模型表现出优异的预测能力。特别是在验证算例2中，模型通过控制互作系数，成功重现了从单调向非单调转变的关键演化过程，解决了长期困扰该领域的双重损伤状态建模问题。

总体而言，该热力学本构模型可有效模拟干热岩在热冲击冷却后的复杂残余强度演化规律，在单调与非单调演化轨迹中均展现出良好适应性。作为一种高鲁棒性数值工具，该模型可广泛应用于地热工程中的井筒稳定性评估与热储层完整性管理，提升地热系统运行的安全性与可靠性，并为多物理场耦合下的岩石本构行为研究提供全新路径。

来源：地热学术观察公众号